Pentagon Calculator

Pentagon Calculator

Pentagon calculator is an online tool that is used to calculate the various properties of a pentagon. It can calculate the area, perimeter, diagonal, and side of a pentagon. This calculator makes the complex geometrical calculation very easy by offering the solutions at one click. We will discuss pentagon, its formulas, and much more in this space. If you are curious about pentagon calculations, keep reading because we are going to discuss several details about pentagon in this post.

How to use the pentagon calculator?

Pentagon calculator not only eliminates the manual calculations but also provides a simple interface to make your calculations super-fast. To use this calculator, follow the below steps:

• Select the property for which you want to solve form the given list, i.e., area, perimeter, diagonal, etc.
• Select the value of pentagon which you already have.
• Now, enter the value for the selected property in the given input box. You can select the unit for the value from centimeter, meter, yard, feet, inches, and kilometer, etc.
• Press the Calculate button after entering the values.

The area of pentagon calculator instantly calculates the properties of pentagon using the given values. It also provides the formula and step by step calculation using that formula. This calculator is very helpful for students who find geometry as a difficult topic. Students can learn the concept of a pentagon by using this calculator.

What is a pentagon?

Pentagon is the five-sided geometrical shape. It is a polygon with five sides and five corners. A pentagon will be a regular pentagon if all of its sides are equal in length and all of its angles are equal. The image below is a regular pentagon with equal size of sides and angles:

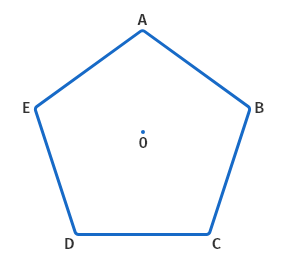
There are a total of four types of pentagon:

Regular Pentagon:

A geometrical shape with five equal sizes of sides and equal size of angles.

Irregular Pentagon:

A geometrical shape with five unequal sizes of sides and unequal size of angles.

Convex Pentagon:

If a pentagon has no internal angle greater than 180 degree, it is a convex pentagon.

Concave Pentagon:

If a pentagon has an internal angle greater than 180 degree, it is a concave pentagon.

Pentagon formulas

Here are the formulas for various properties of pentagon:

Area of pentagon formula

Pentagon area can be calculated by using the below formula:

\(\text{A}=\dfrac{a^2}{4}\times\sqrt{\left(25+10\times \sqrt{5}\right)}\)

In this equation:

A refers to the area of the pentagon, and

a refers to the side of the pentagon.

Perimeter of pentagon formula

\(\text{p} = 5 \times\text{a}\)

In this equation:

p refers to the perimeter of the pentagon, and

a refers to the side of the pentagon

Diagonal of pentagon formula

Pentagon diagonal can be calculated by using the below formula:

\(\text{d}=\dfrac{a} {2}\times\left(1 + \sqrt{5}\right)\)

In this equation:

d refers to the diagonal of the pentagon,

a refers to the side of the pentagon

Height of pentagon formula

Pentagon height can be calculated by using the below formula:

\(\text{h}=\dfrac{a}{2}\times \sqrt{\left(5 + 2\times \sqrt{5}\right)}\)

In this equation:

h refers to the height of pentagon, and

a refers to the side of the pentagon

Radius of pentagon formula

A regular pentagon has two types of radius, circumcircle radius and incircle radius.

Circumcircle radius formula for pentagon

Circumcircle radius of pentagon can be calculated by using the below formula:

\(r_i=\dfrac{a}{10}\times\sqrt{\left(50 + 10\times\sqrt{5}\right)}\)

In this equation:

r_c refers to the circumcircle radius of the pentagon, and

a refers to the side of the pentagon

Incircle radius formula for pentagon

Incircle radius of pentagon can be calculated by using the below formula:

\(r_c=\dfrac{a}{10}\times\sqrt{\left(25+10\times\sqrt{5}\right)}\)

In this equation:

r_i refers to the incircle radius of the pentagon, and

a refers to the side of the pentagon

How to calculate area of pentagon?

Area of pentagon can be calculated by using the above formula for pentagon area. Follow these steps to calculate area of pentagon:

1. Identify and write down the side measurement of the pentagon.
2. Write down the pentagon area formula.
3. Substitute the values in the formula and calculate the area of the pentagon.

Example:

Let’s use an example to understand how to find the area of the pentagon. Suppose a regular pentagon has a side of \(6\) cm. Calculate the area of the pentagon.

Solution:

Step 1: Identify and write down the side measurement of the pentagon.

\(\text{a} = 6 \text{cm}\)

Step 2: Write down the pentagon area formula.

\(\text{A}=\dfrac{a^2}{4}\times \sqrt{\left(25+10\times \sqrt{5}\right)}\)

Step 3: Substitute the values in the formula and calculate the area of the pentagon.

\(\text{A}=\dfrac{6^2}{4}\times \sqrt{\left(25+10\times \sqrt{5}\right)}\)

\(\text{A}=\dfrac{36}{4}\times \sqrt{\left(25+10\times \sqrt{5}\right)}\)

\(\text{A} = 61.94 cm^2\)

So, if a pentagon has a side of  \(6\) cm, its area will be \(61.94 cm^2\) approximately.

How to calculate perimeter of pentagon?

Perimeter of pentagon can be calculated by using the above formula for pentagon perimeter. Follow these steps to calculate the perimeter of pentagon:

1. Identify and write down the side measurement of the pentagon.
2. Write down the pentagon perimeter formula.
3. Substitute the values in the formula and calculate the perimeter of the pentagon.

Example:

Let’s use the same example above to understand how to find the perimeter of the pentagon. Suppose a regular pentagon has a side of \(6\) cm. Calculate the perimeter of the pentagon.

Solution:

Step 1: Identify and write down the side measurement of the pentagon.

\(\text{a} = 6 \text{cm}\)

Step 2: Write down the pentagon perimeter formula.

\(\text{p} = 5 \times\text{a}\)

Step 3: Substitute the values in the formula and calculate the perimeter of the pentagon.

\(\text{p} = 5 \times\text{a}\)

\(\text{p} = 5 \times 6\)

\(\text{p} = 30 \text{cm}\)

So, if a pentagon has a side of \(6\) cm, its perimeter will be \(30\) cm approximately. By using the above formulas, you can calculate the diagonal, height, incircle radius, and circumcircle radius of the pentagon in the same way we have calculated its area and perimeter. However, you can always use the above pentagon calculator to save time. You can also use our polygon calculator if you need to calculate the polygon area.