Polygon Calculator

Polygon Calculator

Regular polygon calculator is an online tool to calculate the various properties of a polygon. It can be used to calculate the area of a regular polygon as well as various sided polygons such as 6 sided polygon, 11 sided polygon, or 20 sided shape, etc. It reduces the amount of time and efforts to find the area or any other property of a polygon.

In this post, we will discuss how to use regular polygon calculator, how to find the area of a polygon, polygon area formula and much more.

How to use polygon calculator?

To use our area of polygon calculator, follow the below steps:

• Select the property of polygon from the given list that you want to calculate.
• Select the given value form the list.
• Enter the number of sides of the polygon in the given input box.
• Enter the measurement of the outer side of the polygon.
• Press the Calculate button after entering all values.

Polygon calculator will calculate the selected property of polygon instantly using the given values. It will also show you the formula and step by step method to find the area of a polygon. If you want to calculate the area of a 5 sided polygon like a pentagon, you can use our pentagon calculator any time.

What is a polygon?

A regular polygon has the same length on all its edges and the same size of all its angles like seen in the image below.

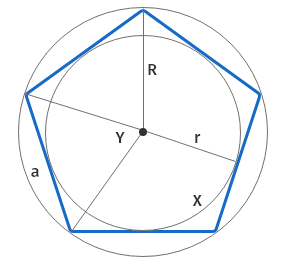
Where:

r refers to the incircle radius or apothem,
R refers to the circumradius,
a refers to the side length, and
x refers to the interior angle

Two specific circles are related to regular polygon.

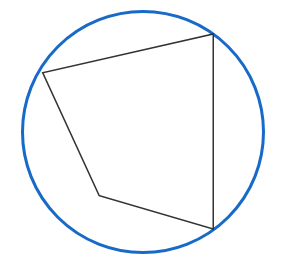
Circumcircle is the circle around the polygon so that all its vertices are touched. When building a polygon, the circle is generally important. In the image below, the orange line is the circumcircle of the polygon.

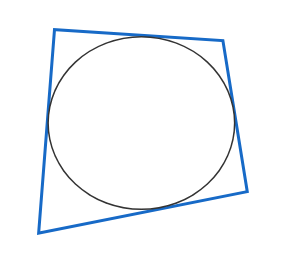
Incircle is the circle drawn around the polygon inside so that all its edges or borders are touched. Refer to the image below for incircle of a polygon. The incircle is shown in orange colour in the picture.

Area of polygon formula

Area of a polygon can be calculated by using the below formula:

A = (1/4) na² cot (π/n) = nr² tan (π/n)

In this equation:

A refers to the area of the polygon,

n refers to the number of sides in polygon,

a refers to the length of the side, and

π is a mathematical constant.

Few more polygon formulas

Here are a few more important polygon formulas and equation for you.

Side Length of polygon (a)

The side length of a regular polygon can be calculated by using the below formula:

a = 2r tan (π/n) = 2R sin (π/n)

In this equation:

r refers to the incircle radius of the polygon, and R refers to the circumcircle radius of the polygon.

Incircle radius of polygon (r)

Incircle radius of a regular polygon can be calculated by using the below formula:

r = (1/2) a cot (π/n) = R cos (π/n)

Circumradius of polygon (R)

Incircle radius of a regular polygon can be calculated by using the below formula:

R = (1/2) a csc (π/n) = r sec (π/n)

Perimeter of polygon (P)

Perimeter of a regular polygon can be calculated by using the below formula:

P = n × a

Interior Angle of polygon (x)

Interior angle of a regular polygon can be calculated by using the below formula:

x = ((n - 2) π / n) radians = (((n - 2) / n) x 180° ) degrees

Exterior Angle of polygon (y)

The exterior angle of a regular polygon can be calculated by using the below formula:

y = (2π / n) radians = (360° / n) degrees

How to find the area of a polygon?

Area of a polygon can be calculated by using the area of a polygon formula. To calculate the area of a regular polygon, follow the below steps:

1. Identify and write down the given values to calculate the polygon area.
2. Write down the formula for polygon area.
3. Substitute the values in the formula to get the area of the polygon.

Example:

Suppose we have a polygon which has each side of 6 cm. There are a total of 7 sides in the polygon. Calculate the area of the polygon.

Solution:

Step 1: Identify and write down the given values to calculate the polygon area. Here we have:

a = 6 cm, n = 7

Step 2: Write down the formula for the polygon area.

A = (1/4) na² cot (π/n) = nr² tan (π/n)

According to the given values, we will use the (1/4) na² cot (π/n) part of the equation. If the radius of the polygon would have been known instead of side length, we should use nr² tan (π/n) part of the equation. Both of them can calculate the area of the polygon.

Step 3: Substitute the values in the formula to get the area of the polygon.

A = (1/4) na² cot (π/n) = (1/4) 7 × 6² cot (3.1415/7)

A = (1/4) × 252 × cot (0.4488) = (1/4) × 252 × 2.07

A = 130.41 cm²

So, a polygon with a total of 7 sides with each side of 6 cm will have an area of 130.41 cm². 7 sided polygons are referred to as septagon. Refer to the below image:

Types of polygon

There are several types of a polygon with the different number of sides such as 11 sided shape, or 8 sided polygon. Refer to the table below for types of the polygon from 3 sided to 20 sided.