Area of a Triangle Calculator
The Triangle area calculator aka sss triangle calculator helps you to calculate the area of a triangle. Not only area but the area of a triangle calculator also gives you the liberty to solve the triangular equation for any value such as:
• Base b
• Area A
• Sides
• Gamma γ
• Parameter
In the post below, you will learn how to find the area of a triangle, how to calculate the length of a triangle, and the formula for the area of a triangle.
By using this right-angle triangle calculator, find the area, base, or height of a triangle. You can calculate the centroid of a triangle using our centroid triangle calculator.
What is a Triangle?
According to Wikipedia
“A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted by ∆ ABC.”
It further states that:
“In Euclidean geometry any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane.”
In the below diagram, A, B, and C are the edges while a, b, and c are the vertices of triangle ABC.
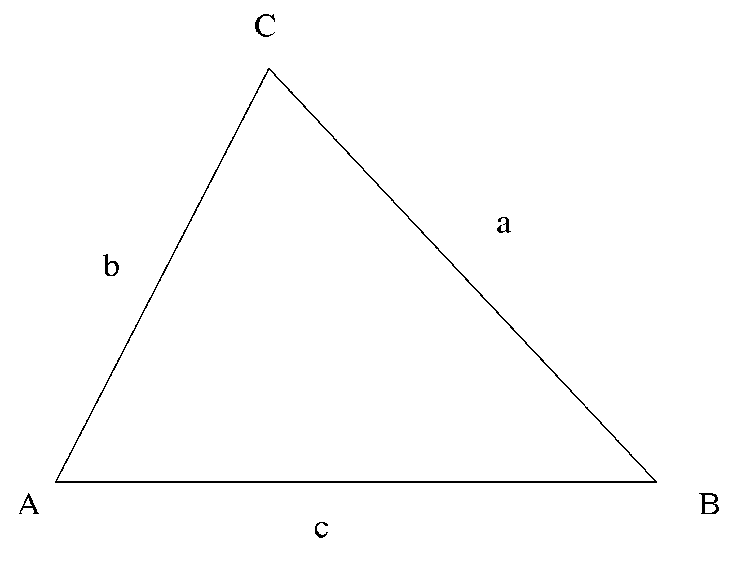
There are several types of triangles and some of those are:
• Equilateral
• Isosceles
• Right-angled triangle
• Scalene
• Obtuse
Formulas of Triangle Calculator
Here is a list of various methods to find the area of a triangle using different equations.
• When base and height are known
If the base b and height h of the triangle are given, its area can be calculated by using the following formula:
Area of triangle = ½ × b × h
• When three sides are known (SSS)
You can use Heron’s formula if all three sides of a triangle are known.
Area = 0.25 × √ ((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))
• When two sides and an angle are known (SAS)
When two sides of a triangle and the angle between them is known, Use the following equation to find the area,
Area = 0.5 × a × b × sin (γ)
• When two angles and a side are known (ASA)
If two angles and a line between them are known, the area of a triangle can be calculated using the above 45 45 90 triangle calculator or the below equation.
Area = a² × sin (β) × sin (γ) / (2 × sin (β + γ))
Note: The above equations contain several trigonometric values. You can use our scientific calculator to evaluate trigonometric values.
How to Find the Area of a Triangle?
You can use this area of a triangle calculator for auto calculation with steps, or you can do it manually too. To find the area of a triangle, follow the below steps:
• Identify and write down the given values.
• Write down the triangle area formula.
• Substitute the given values and calculate the area.
Example:
Find the area of a triangle having a base of 5 cm and a height of 9 cm.
Solution:
Step 1: Identify and write down the given values.
b = 5 cm, h = 9 cm
Step 2: Write down the triangle area formula.
Area of triangle = ½ × b × h
Step 3: Substitute the given values and calculate the area.
Area of triangle = ½ × 5 × 9
Area of triangle = 22.5 cm2
So, the area of this triangle is 22.5 cm2.
You can find the area, base, height, missing side of a triangle, and perimeter of a triangle without manual calculation by using our triangle area calculator. It is a complete triangle calculator, which gives you step-by-step solutions and graph to clearly understand the process of each step. if you are confused to find any missing side or perimeter of a triangle with or without a formula, this free calculator is a perfect choice for you.